神州金庫系統中的裝箱算法

神州控股

龔志峰

神州金庫作為科捷自有研發系統，為客戶提供B2B/B2C全供應鏈提供一體化服務，可前端訂單接入、中端訂單數據處理（OMS、BMS、WMS、TMS等）、大數據處理等，亦可對接智能化設備。通過全國倉包材使用情況統計，發現B2C業務裝箱問題比較突出，一是：包材選用不合理，人工裝箱時沒有邏輯規則概念，導致每年該部分損耗嚴重；二是：箱材的選用影響效率，且準確率低。裝箱問題在倉儲物流行業也是普遍存在的難題，紛紛進行裝箱算法研究。據網上的公開信息，阿里對裝箱問題進行的研究，其物流算法統計，平均可以減少5%的包裝，2017年雙十一發貨量超過10億件，可節省4500多萬個箱子。推行菜鳥電子面單替代傳統三聯面單，阿里電商平臺上商家使用率已經達到80%，每一年節約紙張費用達12億元。科捷依托神州金庫對該方面的問題進行了不斷的研究和探索。

01

關于三維裝箱問題主要從以下幾個方面進行探討

三維裝箱問題算法：

裝箱工人在裝箱過程中需要對訂單的商品選擇箱型，評估商品體積和箱子容積的正確比例，這一過程極其耗費資源，給倉庫作業帶來困難的同時還降低了作業效率。其次，所送商品會出現裝箱不合理的情況，如，顧客只是買一款體積很小的商品，收到的確是一個很大很空的箱子，浪費資源的同時，也給用戶帶來困惑，同時零售商的專業性也遭到了質疑。

三維裝箱規則：

1) 所有箱子均視為標準的長方體或者正方體。長寬高為內圍長寬高。

2) 所有商品均描述為矩形，長寬高為外圍長寬高。

3) 裝箱時，優先放置大件商品。如果大件商品放不滿的情況下，考慮次小商品，直到放滿為止。

4) 裝箱時，優先選擇容積小的箱子。容積更小的箱子如果能夠裝下商品，則剩余容積會更小，說明箱子更適合商品。其次優先選擇常規指數最大的箱子（值越大越常規，值越小表示是非常規箱型甚至是特型箱）。

5) 如果訂單中的商品恰好已經裝完，箱子未滿，嘗試更換容積更小的箱子。如果爆箱則換回原來的箱型。

6) 如果訂單中的商品恰好已經裝完，出現爆箱，嘗試更換小一號箱子，后繼續裝箱剩余商品。如果此時箱子已經是最小，則更換成多個箱子裝箱。

7) 將箱型按照容積從小到大的順序排列。如果箱子裝不滿優先嘗試小的箱型。

8) 箱子優先放置大件商品，然后放置次大商品，最后放訂單中最小的商品。

9) 如果所有的箱子都不能一個箱子裝下單個訂單內的全部商品，才會啟用多個箱子來裝商品。

對一次裝箱過程進行了分解，每次需要一個商品和一個空箱子，同時會產生三塊新的更小的剩余空間。這三塊剩余空間又可以看作是新的箱子。和新的合適自己的空間大小的商品去匹配。

那么，這就是一個遞歸算法，方法輸入一款商品和一個箱子，每一次遞歸都會產生三個新的箱子，新的箱子又可以裝入其它更小的商品。

如此循環往復，直到每一個新的箱子連最小的商品都裝不下了，或者沒有任何商品可以裝進箱子里了，這個過程就會自動結束。這是遞歸的出口條件。

02

目前使用較多的算法

1) Heuristic Algorithm啟發式演算法：工業應用，時間短。用于在合理時間內找到可接受的擺放方式（結果）。

2) Exact Methods精準算法：學術應用，用于研究Global Optimality，Solution Error Bound。最早的數學編程模型，混合整數線性規劃模型，但是，利用整數規劃解決問題不太現實，計算量太大不好實現，很難用線性的求解器去精準解決非線性的問題

3) Three-dimensional open-dimension rectangular packing probloems(3D-ODRPP)。

3D-ODRPP算法詳解：

a) box_selection：選出所有箱子中最小體積的那個；輸入：所有箱子體積；輸出：輸出已打包物品清單，找到的最小箱型；pack_boxes：判斷單個箱子打包所有物品；輸入：單個箱子體積；輸出：輸出已打包物品清單。

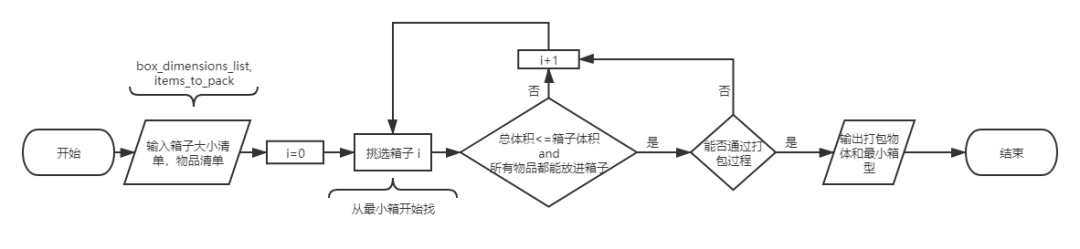
b) pack_boxes：判斷單個箱子打包所有物品；輸入：單個箱子體積；輸出：輸出已打包物品清單；insert_items_into_dimensions：將需要打包的物體塞進給定體積；輸入：剩余長方體體積，需要打包物品，已打包物品；輸出：剩余長方體體積（更新），需要打包物品（更新），已打包物品（更新）。

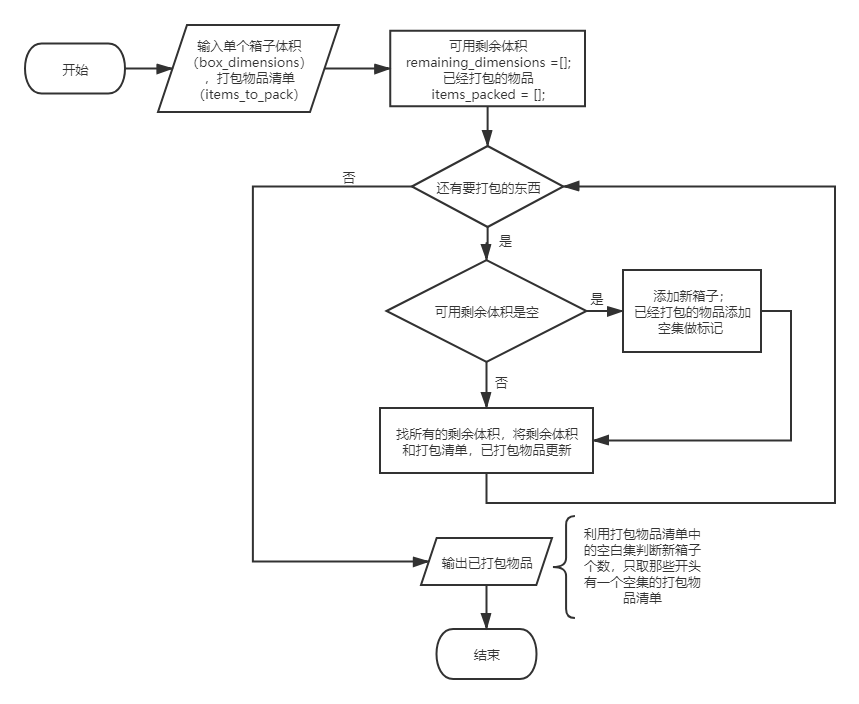
c) insert_items_into_dimensions：將需要打包的所有物體塞進給定體積；輸入：剩余長方體體積，需要打包物品，已打包物品；輸出：剩余長方體體積（更新），需要打包物品（更新），已打包物品（更新）。best_fit：將需要打包單個物體放進給定體積并給出最好切割方法；輸入：給定長方體體積，物品體積；輸出：剩余長方體體積，三個長方體。

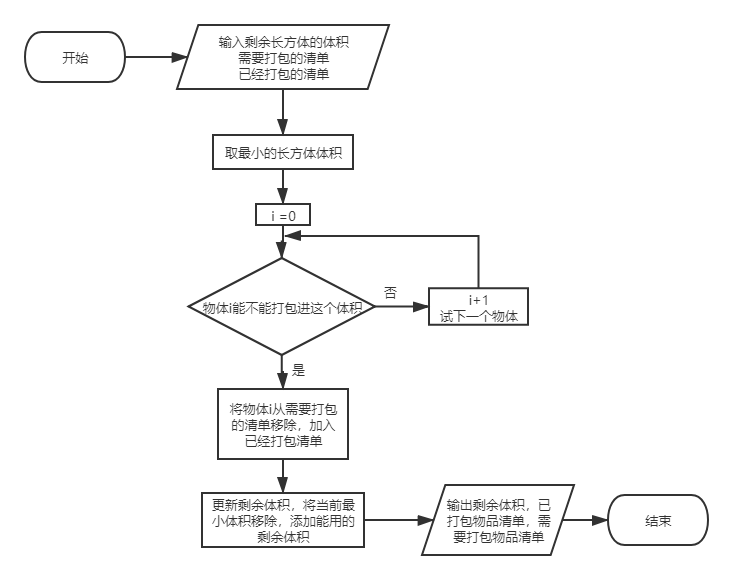
03

針對以上算法進行算法測試設計

對比1：和僅考慮總體積的情況比較。僅考慮體積篩選會選出一些箱型會擺放不開的小箱子，進行篩選和比較。例：物體體積小但特別長。

對比2：和僅考慮總體積+能容納所有物體三邊的情況比較。此種篩選會篩選掉因為物體過長而放不進去的小箱子，依然會選出些擺放不下所有物體的小箱子。例：物體形狀平均但因為位置關系擺放不下。

對比3：先和Ortools的結果對比。因為Ortools跑出來的結果不夠理想，起碼要比Ortools的表現好。從良品鋪子物品清單和沈陽良品-包材維護中抽取隨機訂單，訂單長度（0-6個）。（因為一般的訂單大小都在這個范圍內）看看生成的箱型是否比Ortools的小一些。

04

真實數據測試

選用200個出庫運單，每個運單對應一個箱子，箱子中物體從1到21不等。數據來源沈陽良品庫，9個箱型。已刪除0體積物品（贈品海報一類）。無拆單，拆單率不足1%。

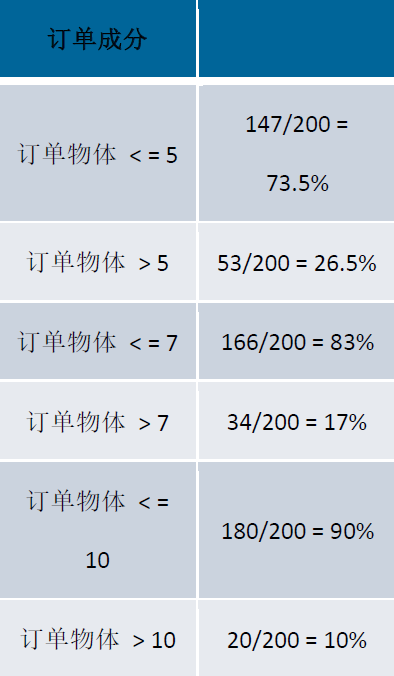
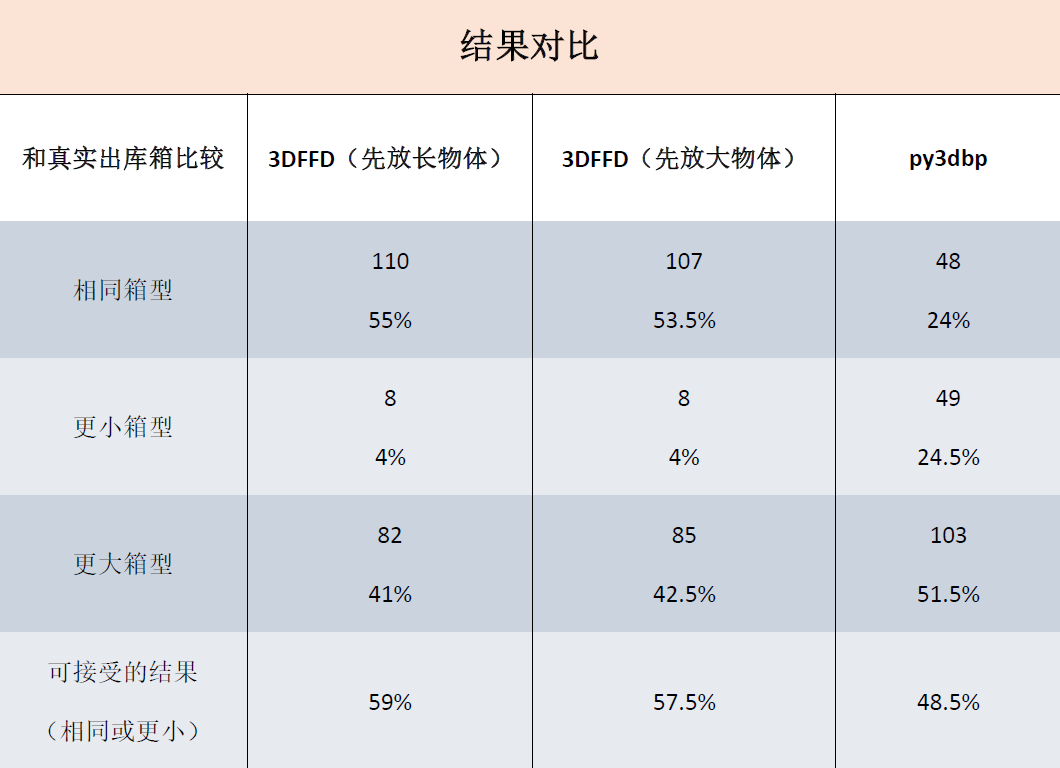
結論：200個出庫運單中，表現最好的是3DFFD先放長物體的策略，和之前隨機訂單生成的測試結果一致。

05

算法表現分析

算法進行的是切割。再拼湊的問題，會直接拋棄掉一些放不進東西的體積（優化）。切割是演變式算法的弊端，不好規避。訂單的物品越少，切割次數越少，效率會越高。和之前隨機訂單生成的測試結果一致，3DFFD是表現最好的算法。對表現不好的案例分析，算法本身的效率不低，差值存在于對物品的擠壓狀況。切割體積造成的問題。